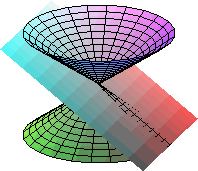
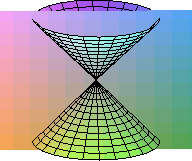
La hipérbola como sección cónica
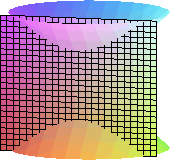
La circunferencia, la elipse, la parábola o la hipérbola son curvas planas de todos conocidas.
Estas curvas aparecían ya en la geometría griega y fueron denominadas secciones cónicas, ya que los griegos de la época de Platón consideraban que tales curvas procedían de la intersección de un cono con un plano.
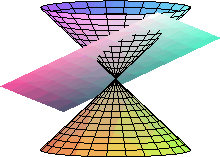
La elipse como sección cónica
Cuando los matemáticos de los siglos XVI y XVII estudiaron los trabajos griegos, empezaron a comprobar la falta de generalidad de los métodos de demostración lo que llevo a sustituir la visión puramente geométrica de las secciones cónicas por otra que incorporaba las nociones de coordenadas y distancia. Esto llevo a la definición de estas curvas como lugares geométricos de puntos que verificaban ciertas propiedades en términos de distancia. (las cónicas como lugares geométricos).
La parábola como sección cónica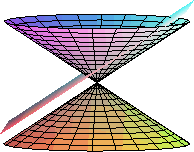
Finalmente se estableció una teoría algebraica general que engloba todas estas curvas y las describe como curvas cuadráticas. Es esta teoría la que presentamos a continuación.
Curvas cuadráticas
Una cónica es el lugar geométrico de los puntos del plano (x,y) que satisfacen una ecuación completa de segundo grado:
La ecuación de una cónica se puede escribir en forma matricial como
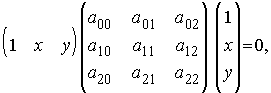
donde
Una cónica queda pues definida por una matriz simétrica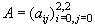
En lo que sigue denotaremos por Aii a la matriz adjunta en A del elemento aii i=0,1,2 .
Ejemplo:
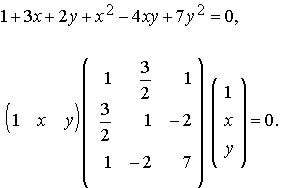
En el siguiente gráfico vemos la cónica que representa la ecuación cuadrática anterior
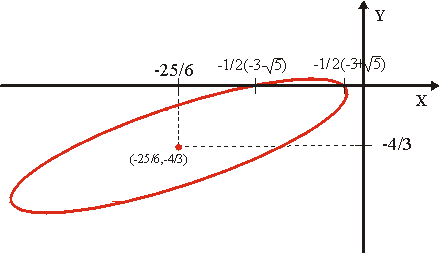
En este caso la matriz de la cónica y las matrices adjuntas correspondientes son
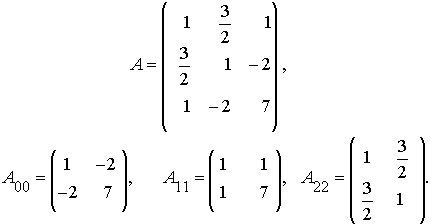
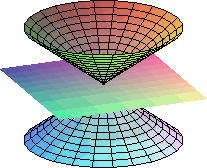
Las figuras que represetan las ecuaciones cuadráticas pueden ser, además de elipses, hipérbolas y parábolas, pares de rectas tanto secantes como paralelas y estas últimas pueden ser distintas o coincidentes. También puede darse el caso de que la ecuación sea verificada por un único punto o por ninguno. Alguna de estas últimas también se pueden obtener como secciones cónicas como se ve en las imágenes siguientes:
A continuación estudiamos como se puede determinar que tipo de curva que define una ecuación cuadrática dada.
Existen ciertas cantidades asociadas a la matriz de la cónica que son invariantes respecto a los movimientos del plano (giros y traslaciones).
Siy
son las matrices asociadas a la cónica después de que ésta ha sufrido un giro y una traslación, respectivamente, entonces
1) det A=det A'=det A'',2) a11 + a22 = a'11+ a'22 = a''11 + a''22,3) det A00 = det A'00 = det A''00.
Tabla de Clasificación det A ≠ 0 |
| ||||||||||||
det A= 0 |
|
Centro:
Polar Dado un punto P=(x0,y0) se llama polar de P respecto de una cónica C de matriz A a la recta de ecuación
Si el punto P está en la cónica C entonces la recta polar de P respecto a C es precisamente la recta tangente a la cónica en dicho punto P.
Ejemplo:
Consideremos la cónica de ecuación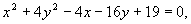
que matricialmente se escribe como
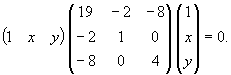Utilizando la tabla de clasificación vemos que se trata de una elipse real puesto que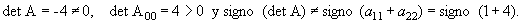
La polar del punto (1,2) será la recta
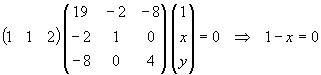
Observamos que el punto (1,2) pertenece a la cónica y por lo tanto la polar coincide con la recta tangente en dicho punto.
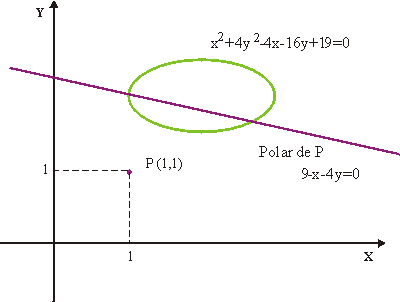
La polar del punto (1,1) es la recta
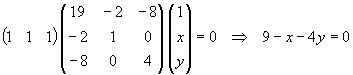
La polar del punto (3/2, 9/4) es la recta
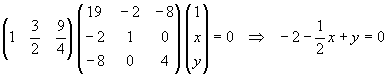
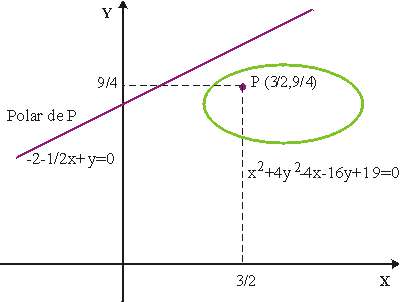
Es posible que un punto P=(x0,y0) no tenga polar respecto a una cónica C. Las coordenadas de los puntos que no tienen polar deben verificar el sistema de ecuaciones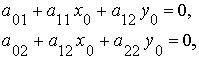
que impone que los coeficientes de x e y en la recta polar sean nulos (es decir que no exista dicha recta).Para que este sistema tenga alguna solución se ha de verificar
Además si det A00 es no nulo, entonces la solución del sistema es única y por lo tanto habría un único punto que no poseerá recta polar. Este punto se denomina centro de la cónica. No todas las cónicas tienen centro.
El centro de la cónica tiene la particularidad de ser su centro de simetría.
Si C es una elipse o una hipérbola entonces det A00 ≠ 0 y el sistema es compatible determinado lo que indica que estas cónicas tienen centro y que éste es único.
Ejemplo:
En la elipse del ejemplo anterior el centro será el punto (2,2) única solución del sistema de ecuaciones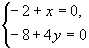
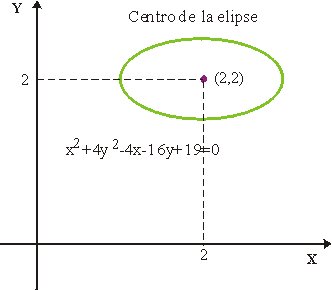
Sin embargo si la cónica es una parábola, todos sus puntos tienen polar. La parábola es por tanto una cónica sin centro.
Polo Dada una recta r diremos que un punto P es un polo de r respecto a una cónica C si r es la polar de P respecto a C
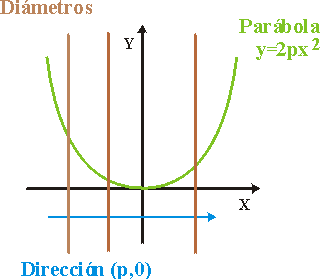
Por supuesto hay rectas que no tienen polos: en la elipse y la hipérbola son todas las que pasan por el centro y en la parábola son las rectas de dirección (-a12, a11) que son además perpendiculares al vector (a01 a12 - a02 a11, a01 a22 - a02 a12) y las únicas que cortan a la parábola en un solo punto.Diámetro Llamaremos diámetro de una cónica C a cualquier recta sin polo.
Las figuras siguientes muestran diámetros en una elipse y una parábola
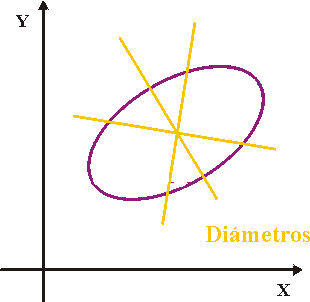
Diremos que dos diámetros son conjugados si no son asíntotas (en el caso de la hipérbola) y uno de ellos coincide con el lugar geométrico de los puntos medios de las cuerdas determinadas por la cónica en las rectas paralelas al otro.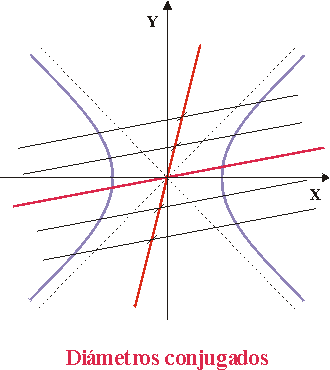
La ecuación reducida de una cónica es aquella ecuación simplificada de la curva que sitúa el centro (si lo tiene) de la cónica como origen de coordenadas mientras que los ejes presentan unas relaciones particulares con la cónica.
Partiendo de la ecuación general de una cónica se puede llegar a su ecuación reducida aplicándole consecutivamente un giro y una traslación de forma adecuada.Clasificaremos en tres tipos las ecuaciones reducidas de las cónicas:
- Elipse, hipérbola, pares de rectas no paralelas:
Donde a'11 y a'22 son las soluciones de la ecuación en z
y
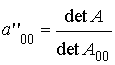
- Parábola
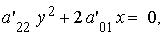con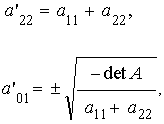
- Pares de rectas paralelas o coincidentes
con
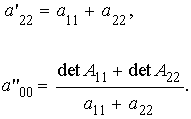
Ejemplo:
Consideremos la ecuación cuadrática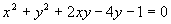
La matriz de la cónica que define la ecuación anterior será
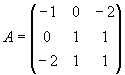Veamos que tipo de cónica es calculando sus invariantes
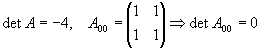Esto nos indica que es una parábola.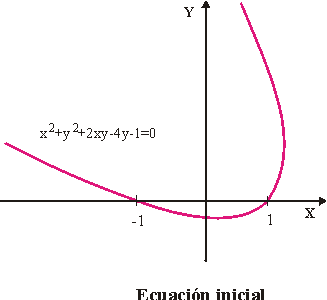
La ecuación reducida de esta parábola será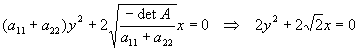
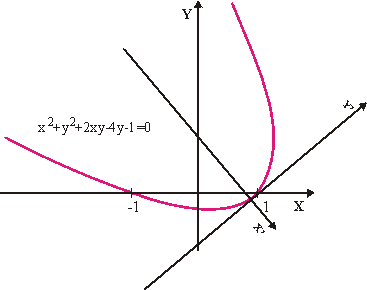
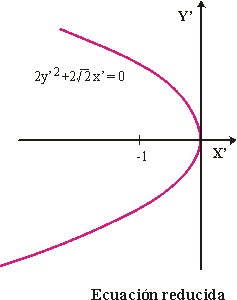
Las cónicas como lugares geométricos
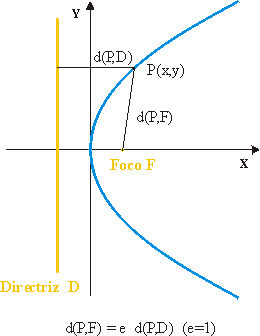
Si F es un punto fijo del plano y D una recta, el lugar geométrico de los puntos del plano cuyas distancias al punto F y a la recta D están en proporción constante es una cónica no degenerada (elipse, hipérbola, parábola).Al punto F se le denomina foco de la cónica y a la recta D directriz asociada al foco F.
Ecuación focal
Si C es una cónica propia (no degenerada), en un sistema de referencia determinado, su ecuación será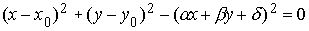
donde F=(x0, y0) es el foco de la cónica y la recta ax+by+d=0 es la directriz asociada al foco F. La ecuación anterior se puede transformar fácilmente en
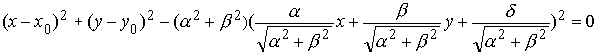Renombrando los coeficientes y haciendo a2+b2=e2 ya que a2+b2 >0 la ecuación queda finalmente como
Esta ecuación se conoce como ecuación focal de la cónica y a'x+b'y+d'=0 es la ecuación de Euler para la directriz. Más adelante veremos como se puede obtener la ecuación focal partiendo de la ecuación reducida de la cónica.
La cantidad e se denomina excentricidad de la cónica y es un invariante puesto que, como se comprueba fácilmente, det A00=1-e2
En términos de distancia, la ecuación focal queda como
Es decir, en una cónica no degenerada el cociente entre las distancias de cualquiera de sus puntos al foco y a la directriz es constante (dada por la excentricidad).
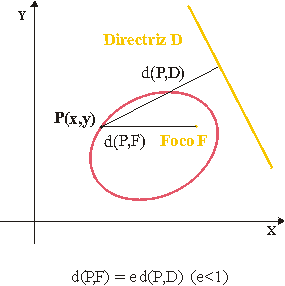
Se puede comprobar que en una cónica la directriz asociada a un foco F es precisamente su recta polar. El foco de la cónica es pues cualquier punto del plano para el que la razón de la distancia de un punto cualquiera P de la cónica a F y la distancia de P a la polar de F es constante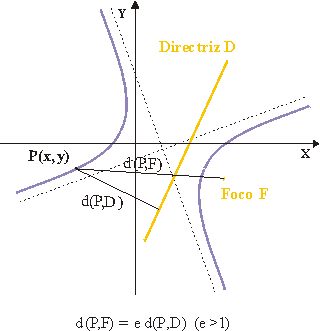
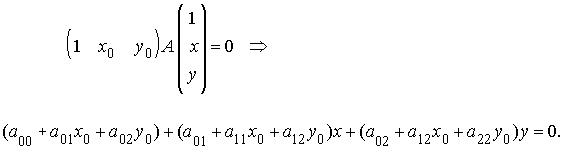
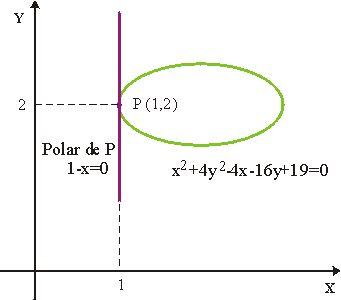
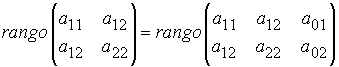
No hay comentarios:
Publicar un comentario